小倉キャンパス ブログ

通信制　一ツ葉高校　小倉キャンパスです。

こんにちは。また、暑い日が戻ってきましたね～(^^;)。日焼け対策には十分に気を付けている柳尾です(笑)。

今日は８月31日、あっという間に８月最後の日ですね。

昨日から前期の残りの授業が再開されています。先生たちもしっかりサポートしますので、一緒に頑張っていきましょう！

さて、今日は海洋調査シリーズ第三弾、遂に最終回です(TT)。それで、ちょっと真面目にいってみようと思います（笑）。

『海』と聞くと、皆さんはどんな事を思い浮かべますか？

生徒などに聞いて一番多いのは、お魚、イルカさんなどの生き物系です。マリンスポーツが好きな人も多いでしょうから、サーフィンやヨットを思い浮かべる人もいるでしょう。中には、海辺をデートしたあの日のことを思い出す人もいるかもしれません(^^;)

では私はというと、真っ先に波や海流を思い浮かべます(^o^)。

物理を選択している人はすぐにピントくると思いますが、波というと正弦波→三角関数を思い浮かべるのではないでしょうか。

また海流と言えば、これはちょっと難しいかもしれませんが、実は地球自転の効果によって生じるコリオリ力と海の水位差によって生じる圧力勾配力との運動方程式で表せるのです。

つまり、『海』は実は物理や数学と非常に関係が深いのです。

そこで今日は、私が先月に行った海洋調査の時にどんなことをやっていたかを少しだけ紹介します。

その一つが、海の中の流れの速さを測り、そのデータ処理を行うことでした。

この海水の流動は航走する船から連続観測する事ができます。これには、船に搭載されているドップラー流速計（ADCP；Acoustic Doppler Current Profiler)という機器を使います。

測定されたデータは、流れの方向と大きさという二つの要素です。

そうです！　方向と大きさ、それはまさにベクトルですね。

では、船が航走しながら時々刻々と変化する流速のベクトルを描くにはどうしたら良いでしょうか!?

ベクトルを描くには、始点と終点の座標を決めなければなりません。

始点は船の位置、終点は流速ベクトルを東西(X)方向成分と南北(Y)方向成分に分解すると分かります。流れの大きさをV、そのX成分、Y成分をそれぞれV_x 、V_y とすると、V_x=Vcosθ、V_y=Vsinθ　となります。

ここで、ちょっと注意しなければならないのは、ベクトルの始点は船と共に常に移動していること。もう一つは、方向の表し方は真北の時にθ=0°なので、真東ではθ=90°になるという事です。

という訳で、ある海域で測定したデータを処理し、流速ベクトルを作図すると下図の様になります。

これは、北太平洋の南方海域において観測した水深177mの流速ベクトル分布です。

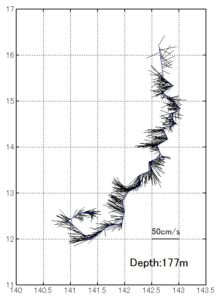
この様に、数学や物理は海の分野でもすごく役に立つのです。

将来、海洋の分野に進みたい人は、生物だけでなく数学や物理も是非興味をもって勉強して下さいね！

逆に数学が好きな人は、海洋の分野でそれを大いに役立てる事ができますよ(^^)/

通信制一ツ葉高校　小倉キャンパス　柳尾